
Do your students struggle with common linear equations and inequalities mistakes? I know mine did before I started using these strategies in my classroom. Here are my strategies for combating the top four linear equations and inequalities mistakes that I see students make!
Linear Equations and Inequalities Mistake #1
With linear equations and inequalities, students confuse m and b when the order is switched in slope-intercept form.
Solution: Tell your students that m(slope) and x go together like: shoes and socks, bees and honey, toothbrush and toothpaste, etc. (you can even have students come up with their own analogy to help them remember!) And because of this the b feels left out and says WHY(Y)?? This will help them remember the b represents the y-intercept!
So whether you have have:
y= 5x – 6 OR y=-6+5x
The slope is 5 and the y-intercept is -6
Linear Equations and Inequalities Mistake #2
Assuming that horizontal lines are represented by x= while vertical lines are represented by y= in linear equations and inequalities.
Tip: Use a mnemonic device to help students remember that horizontal lines are represented by y= because they are parallel to the x-axis AND vertical lines are represented by x= because they are parallel to the y-axis.
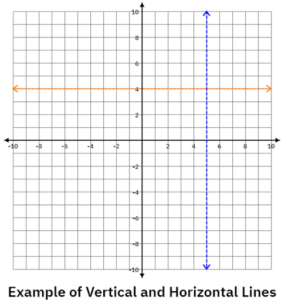
HOY
Horizontal Graph
Slope=0
Use y= for the equation
VUX
Vertical Graph
Slope=Undefined
Use x= for the equation
Linear Equations and Inequalities Mistake #3
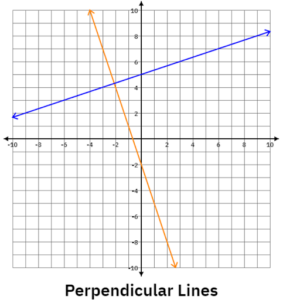
Students use the reciprocal instead of the negative reciprocal when finding perpendicular lines.
Tip: First, make sure that students know the meaning of perpendicular. Then use a visual example to show that one slope must be positive and one negative for them to intersect at a 90 degree angle. This can save a lot of headaches down the road! See the example below.
Linear Equations and Inequalities Mistake #4
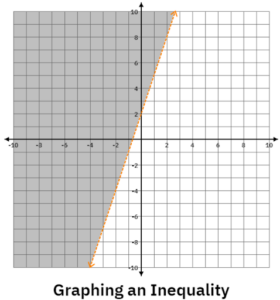
Students shade the wrong side when graphing inequalities.
Tip: Have students solve each inequality for y. Have them shade BELOW the line if the inequality symbol is < or ≤. If the inequality symbol is > or ≥, have them shade ABOVE the line. Then if the equation is in standard form, use a test point and SHADE where the point is TRUE for the inequality.
By using these strategies, I have decreased the number of errors students make with linear equations and inequalities significantly! Which tip will you use in your classroom? Let me know in the comments!
Looking for more resources to help teach linear equations and inequalities?
Grab this freebie to get started!
OR check out these other resources to help you!
Identifying Parallel and Perpendicular Lines: $100,000 Pyramid Activity
Error Analysis of Graphing Linear Inequalities
Error Analysis of Solving for y and Graphing Linear Equations
Error Analysis of Solving Equations in Slope-Intercept Form using y = mx + b to find b





